Structured Natural Gradient Descent (ICML 2021)

12 minute read

More about this work [1]: Long talk, (Youtube) short talk, extended paper, short paper, poster

Introduction

Motivation

Many problems in optimization, search, and inference can be solved via natural-gradient descent (NGD)

Structures play an essential role in

  • Preconditioners of first-order and second-order optimization, gradient-free search.
  • Covariance matrices of variational Gaussian inference [2]

Natural-gradient descent on structured parameter spaces is computationally challenging.

Limitations of existing NGD methods:

  • Limited structures due to the complicated Fisher information matrix (FIM)
  • Ad-hoc approximations for handling the singular FIM and cost reductions
  • Inefficient and complicated natural-gradient computation
Existing approach for rank-one covariance Our NGD for rank-one covariance

Our Contributions

We propose a flexible and efficient NGD method to incorporate structures via matrix Lie groups.

Our NGD method

  • generalizes the exponential natural evolutionary strategy [3]
  • recovers existing Newton-like algorithms
  • yields new structured 2nd-order methods and adaptive-gradient methods with group-structural invariance [4]
  • gives new NGD updates to learn structured covariances of Gaussian, Wishart and their mixtures
  • is a systematic approach to incorporate a range of structures

Applications of our method:

  • deep learning (structured adaptive-gradient),
  • non-convex optimization (structured 2nd-order),
  • evolution strategies (structured gradient-free),
  • variational mixture of Gaussians (Monte Carlo gradients for structured covariance).

NGD for Optimization, Inference, and Search

A unified view for problems in optimization, inference, and search as optimization over (variational) parametric family $q(w|\tau)$: $$ \begin{aligned} \min_{ \tau \in \Omega_\tau } \mathcal{L}(\tau):= \mathrm{E}_{q(\text{w}| \tau )} \big[ \ell(\mathbf{w}) \big] + \gamma \mathrm{E}_{q(\text{w} |\tau )} \big[ \log q(w|\tau) \big] \end{aligned} \tag{1}\label{1} $$ where $\mathbf{w}$ is the decision variable, $\ell(\mathbf{w})$ is a loss function, $\Omega_\tau$ is the parameter space of $q$, and $\gamma\ge 0$ is a constant.

Using gradient descent and natural-gradient descent to solve $\eqref{1}$: $$ \begin{aligned} \textrm{GD: } &\tau_{t+1} \leftarrow \tau_t - \alpha \nabla_{\tau_t} \mathcal{L}(\tau) \\ \textrm{Standard NGD: } & \tau_{t+1} \leftarrow \tau_t - \beta\,\, \big[ \mathbf{F}_{\tau} (\tau_t) \big]^{-1} \nabla_{\tau_t} \mathcal{L}(\tau) \end{aligned} $$ where $\mathbf{F}_{\tau} (\tau_t)$ is the FIM of distribution $q(w|\tau)$ at $\tau=\tau_t$. For an introduction to natural-gradient methods, see this blog.

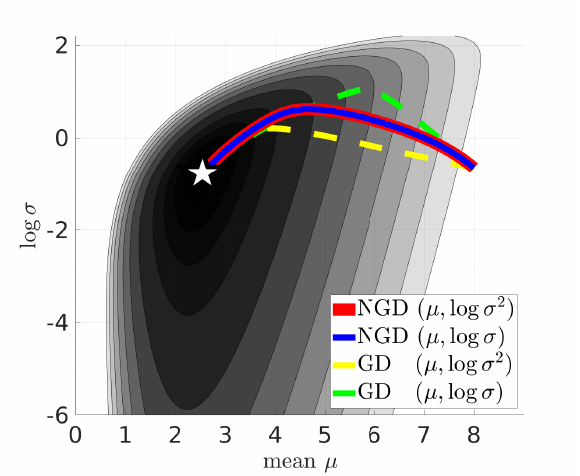
Advantages of NGD:

  • recovers a Newton-like update for Gaussian family $q(\mathbf{w}|\mu,\mathbf{S})$ with parameter $\tau=(\mu,\mathbf{S})$, mean $\mu$, and precision $\mathbf{S}$. $$ \begin{aligned} \mu_{t+1} & \leftarrow \mu_t - \beta \mathbf{S}_{t}^{-1} E_{q(\text{w}|\tau_t)}{ \big[ \nabla_w \ell( \mathbf{w}) \big] } \\ \mathbf{S}_{t+1} & \leftarrow (1-\beta \gamma)\mathbf{S}_t + \beta E_{q(\text{w}|\tau_t)}{ \big[ \nabla_w^2 \ell(\mathbf{w}) \big] } \end{aligned} \tag{2}\label{2} $$
  • is less sensitive to parameter transformations than GD
  • converges faster than GD

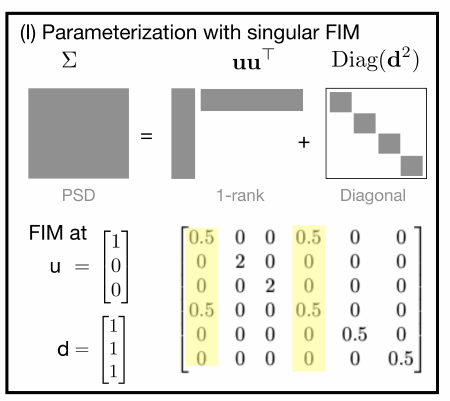
Challenges of standard NGD:

  • NGD could violate parameterization constraints (e.g., $\mathbf{S}_{t+1}$ in $\eqref{2}$ may not be positive-definite)
  • Singular Fisher information matrix (FIM) $\mathbf{F}_{\tau}(\tau)$ of $q(w|\tau)$
  • Limited precision/covariance structures
  • Ad-hoc approximations for cost reductions
  • Complicated and inefficient natural-gradient computation

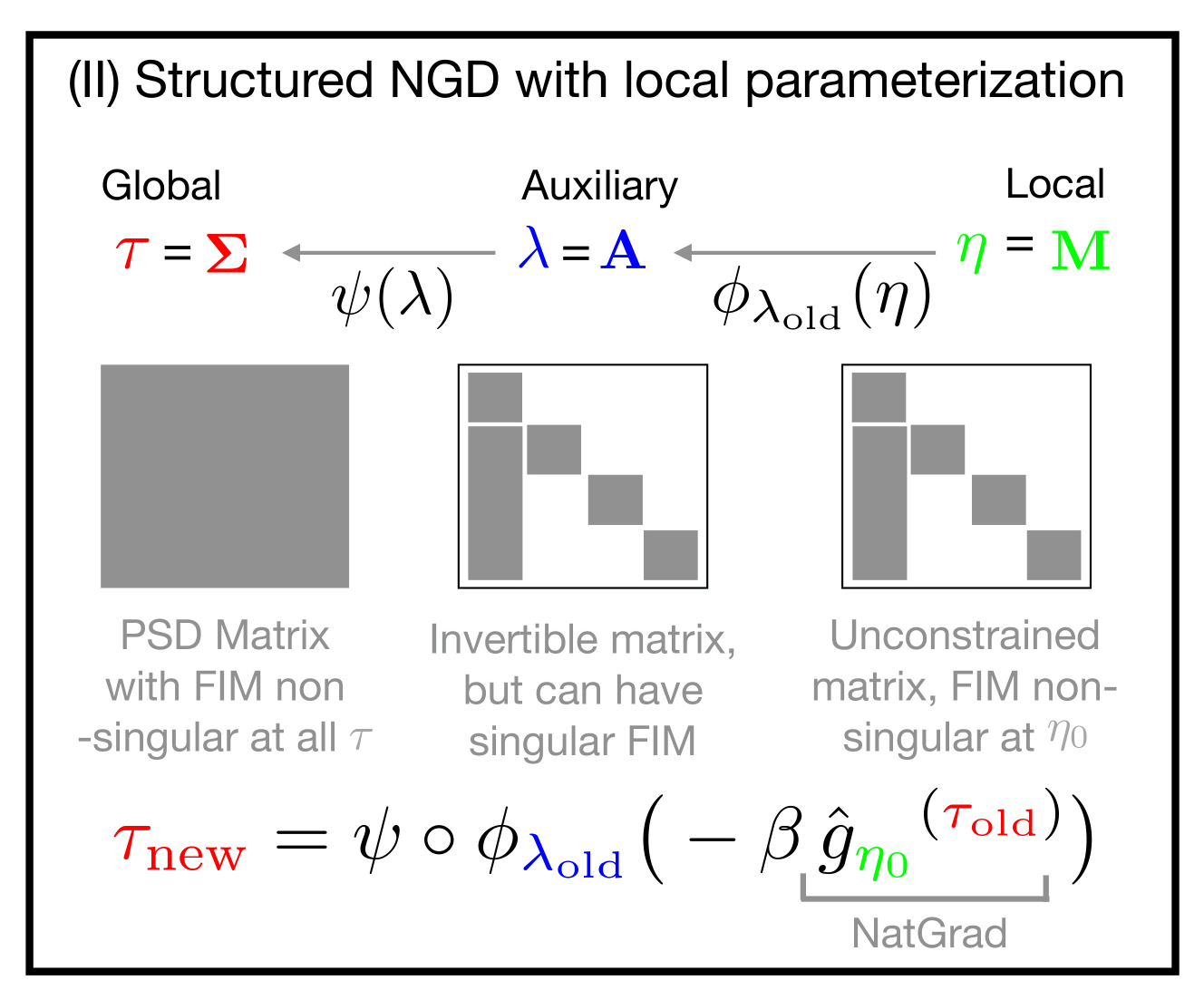
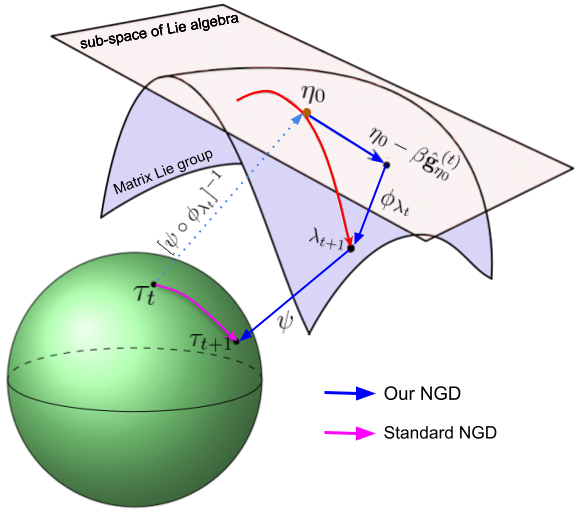
NGD using Local Parameterizations

Our method performs NGD updates in local parameter $\eta$ while maintaining structures via matrix groups in auxiliary parameter $\lambda$. This decoupling enables a tractable update that exploits the structures in auxiliary parameter spaces.

When $\tau$ space has a local vector-space structure,
standard NGD in $\tau$ space is a special case of our NGD,
where we choose $\psi$ to be the identity map and $\phi_{\lambda_t}$ to be a linear map.

We consider the following three kinds of parameterizations.

  • Global (original) parameterization $\tau$ for $q(w|\tau)$
  • New auxiliary parameterization $\lambda$ with a surjective map: $\tau= \psi(\lambda)$
  • Local parameterization $\eta$ for $\lambda$ at a current value $\lambda_t$ with a local map: $\lambda = \phi_{\lambda_t} (\eta)$,
    where $\phi_{\lambda_t}$ is tight at $\lambda_t$: $\lambda_t \equiv \phi_{\lambda_t} (\eta_0)$, and we assume $\eta_0 =\mathbf{0}$ to be a relative origin.
Our NGD:

$$ \begin{aligned} \lambda_{t+1} & \leftarrow \phi_{\lambda_t} \big( \overbrace{\eta_0-\beta \hat{\mathbf{g}}_{\eta_0}^{(t)} }^{ \text{NGD in local space} } \big) \,\,\,\, \textrm{(structure-preserving update in auxiliary space)}\\ \tau_{t+1} & \leftarrow \psi\big( \lambda_{t+1} \big) \,\,\,\, \textrm{(constraint-satisfaction update in global space)} \end{aligned} $$

where $\hat{\mathbf{g}}_{\eta_0}^{(t)}$ is the natural-gradient $\hat{\mathbf{g}}_{\eta_0}^{(t)}$ at $\eta_0$ tied to $\lambda_t$, which is computed by the chain rule, $$ \begin{aligned} \hat{\mathbf{g}}_{\eta_0}^{(t)} &= {\color{green}\mathbf{F}_{\eta}(\eta_0)^{-1} } \,\, \big[ \nabla_{\eta_0} \big[ \psi \circ \phi_{\lambda_t} (\eta) \big] \nabla_{\tau_t}\mathcal{L}(\tau) \big] \end{aligned} $$ where $\mathbf{F}_{\eta}(\eta_0)$ is the (exact) FIM for $\eta_0$ tied to $\lambda_t$. Our method allows us to choose map $\psi \circ \phi_{\lambda_t}$ so that the FIM $\mathbf{F}_{\eta}(\eta_0)$ is easy to inverse at $\eta_0$, which enables tractable natural-gradient computation.

Gaussian Example with Full Precision

Notations:

  • $\mathrm{GL}^{p\times p}$: Invertible Matrices (General Linear Group),
  • $\mathcal{D}^{p\times p}$: Diagonal Matrices,
  • $\mathcal{D}_{++}^{p\times p}$: Diagonal and invertible Matrices (Diagonal Matrix Group),
  • $\mathcal{S}_{++}^{p\times p}$: (Symmetric) positive-definite Matrices,
  • $\mathcal{S}^{p\times p}$: Symmetric Matrices.

Consider a Gaussian family $q(w|\mu,\mathbf{S})$ with mean $\mu$ and precision $\mathbf{S}=\Sigma^{-1}$.

The global, auxiliary, and local parameterizations are: $$ \begin{aligned} \tau &= \Big\{\mu \in \mathcal{R}^p, \mathbf{S} \in \mathcal{S}_{++}^{p\times p} \Big\}, & \mathbf{S}: \text{positive-definite matrix} \\ \lambda & = \Big\{ \mu \in \mathcal{R}^p , \mathbf{B} \in\mathrm{GL}^{p\times p} \Big\}, &\mathbf{B}: \text{ (closed, connected) matrix Lie group member}\\ \eta &= \Big\{ \delta\in \mathcal{R}^p, \mathbf{M} \in\mathcal{S}^{p\times p} \Big\}, & \mathbf{M}: \text{ member in a sub-space of Lie algebra} \end{aligned} $$

Define $\mathbf{h}(\mathbf{M}):=\mathbf{I}+\mathbf{M}+\frac{1}{2} \mathbf{M}^2$. Maps $\psi$ and $\phi_{\lambda_t}$ are : $$ \begin{aligned} \Big\{ \begin{array}{c} \mu \\ \mathbf{S} \end{array} \Big\} = \psi(\lambda) & := \Big \{ \begin{array}{c} \mu \\ \mathbf{B}\mathbf{B}^\top \end{array} \Big \}, \\ \Big \{ \begin{array}{c} \mu \\ \mathbf{B} \end{array} \Big \} = \phi_{\lambda_t}(\eta) & := \Big \{ \begin{array}{c} \mu_t + \mathbf{B}_t^{-T} \delta \\ \mathbf{B}_t \mathbf{h} (\mathbf{M}) \end{array} \Big \}. \end{aligned} \tag{3}\label{3} $$

We propose using Lie-group retraction map $\mathbf{h}()$ to

  • keep natural-gradient computation tractable
  • maintain numerical stability
  • enable lower iteration cost compared to the matrix exponential map suggested in [3]

Our NGD update in $ \lambda $ space is shown below, where we assume $\eta_0=\mathbf{0}$. $$ \begin{aligned} \Big\{ \begin{array}{c} \mu_{t+1} \\ \mathbf{B}_{t+1} \end{array} \Big\} = \lambda_{t+1} = \phi_{\lambda_t} \big( \eta_0-\beta \hat{\mathbf{g}}_{\eta_0}^{(t)} \big) =\Big\{ \begin{array}{c} \mu_t - \beta \mathbf{B}_{t}^{-T} \mathbf{B}_t^{-1} \mathbf{g}_{\mu_t} \\ \mathbf{B}_t \mathbf{h}\big(\beta \mathbf{B}_t^{-1}\mathbf{g}_{\Sigma_t} \mathbf{B}_t^{-T} \big) \end{array} \Big\} \end{aligned} $$ where tractable natural-gradient $\hat{\mathbf{g}}_{\eta_0}^{(t)}$ at $\eta_0=\{\delta_0, \mathbf{M}_0\}$ tied to $\lambda_t=\{\mu_t,\mathbf{B}_t\}$ is

$$ \begin{aligned} \hat{\mathbf{g}}_{\eta_0}^{(t)} = \Big( \begin{array}{c} \hat{\mathbf{g}}_{\delta_0}^{(t)}\\ \mathrm{vec}( \hat{\mathbf{g}}_{M_0}^{(t)})\end{array} \Big) = \underbrace{ {\color{green} \Big(\begin{array}{cc} \mathbf{I}_p & 0 \\ 0 & 2 \mathbf{I}_{p^2} \end{array} \Big)^{-1}} }_{ \text{inverse of the exact FIM } } \Big[\begin{array}{c} \mathbf{B}_t^{-1} \mathbf{g}_{\mu_t} \\ \mathrm{vec}( -2\mathbf{B}_t^{-1} \mathbf{g}_{\Sigma_t} \mathbf{B}_t^{-T}) \end{array} \Big] \,\,\,\,& (\text{tractable: easy to inverse FIM at } \eta_0) \end{aligned} $$

Note that $\mathbf{g}_\mu$ and $\mathbf{g}_{\Sigma}$ are Euclidean gradients of $\eqref{1}$ computed via Stein’s lemma [2] [5] : $$ \begin{aligned} \mathbf{g}_\mu = \nabla_{\mu}\mathcal{L}(\tau) = E_{q}{ \big[ \nabla_w \ell( \mathbf{w} ) \big] }, \,\,\,\,\, \mathbf{g}_{\Sigma} = \nabla_{S^{-1}}\mathcal{L}(\tau) = \frac{1}{2} E_{q}{ \big[ \nabla_w^2 \ell( \mathbf{w}) \big] } - \frac{\gamma}{2} \mathbf{S} \end{aligned} \tag{4}\label{4} $$

Our update on $\mathbf{S}_{t+1}=\mathbf{B}_{t+1}\mathbf{B}_{t+1}^T$ and $\mu_{t+1}$ is like update of $\eqref{2}$ as $$ \begin{aligned} & \mu_{t+1} = \mu_t - \beta \mathbf{S}_{t}^{-1} E_{q(\text{w}|\tau_t)}{ \big[ \nabla_w \ell( \mathbf{w} ) \big] } \\ &\mathbf{S}_{t+1} = \underbrace{ \overbrace{(1-\beta \gamma)\mathbf{S}_t + \beta E_{q(w|\tau_t)}{ \big[ \nabla_w^2 \ell(\mathbf{w}) \big] }}^{\text{standard NGD on $\mathbf{S}$ }} + { \color{red} \frac{\beta^2}{2} \mathbf{G}_t \mathbf{S}_t^{-1}\mathbf{G}_t} }_{\color{red}{\text{ RGD with retraction}}}+ O(\beta^3) \end{aligned} $$ where $\mathbf{B}$ is a dense matrix in matrix group $\mathrm{GL}^{p\times p}$ and $\mathbf{G}_t := E_{q(w|\tau_t)}{ \big[ \nabla_w^2 \ell(\mathbf{w}) ] } -\gamma \mathbf{S}_t$.

The second-order term shown in red is used for the positive-definite constraint [6] known as a retraction in Riemannian gradient descent (RGD). The higher-order term $O(\beta^3)$ will be used for structured precision matrices in the next section.

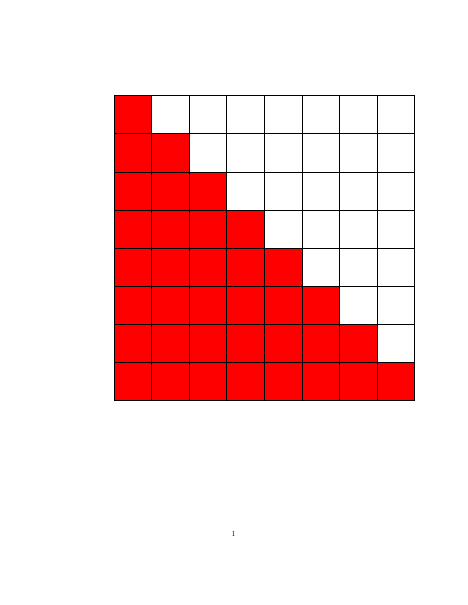
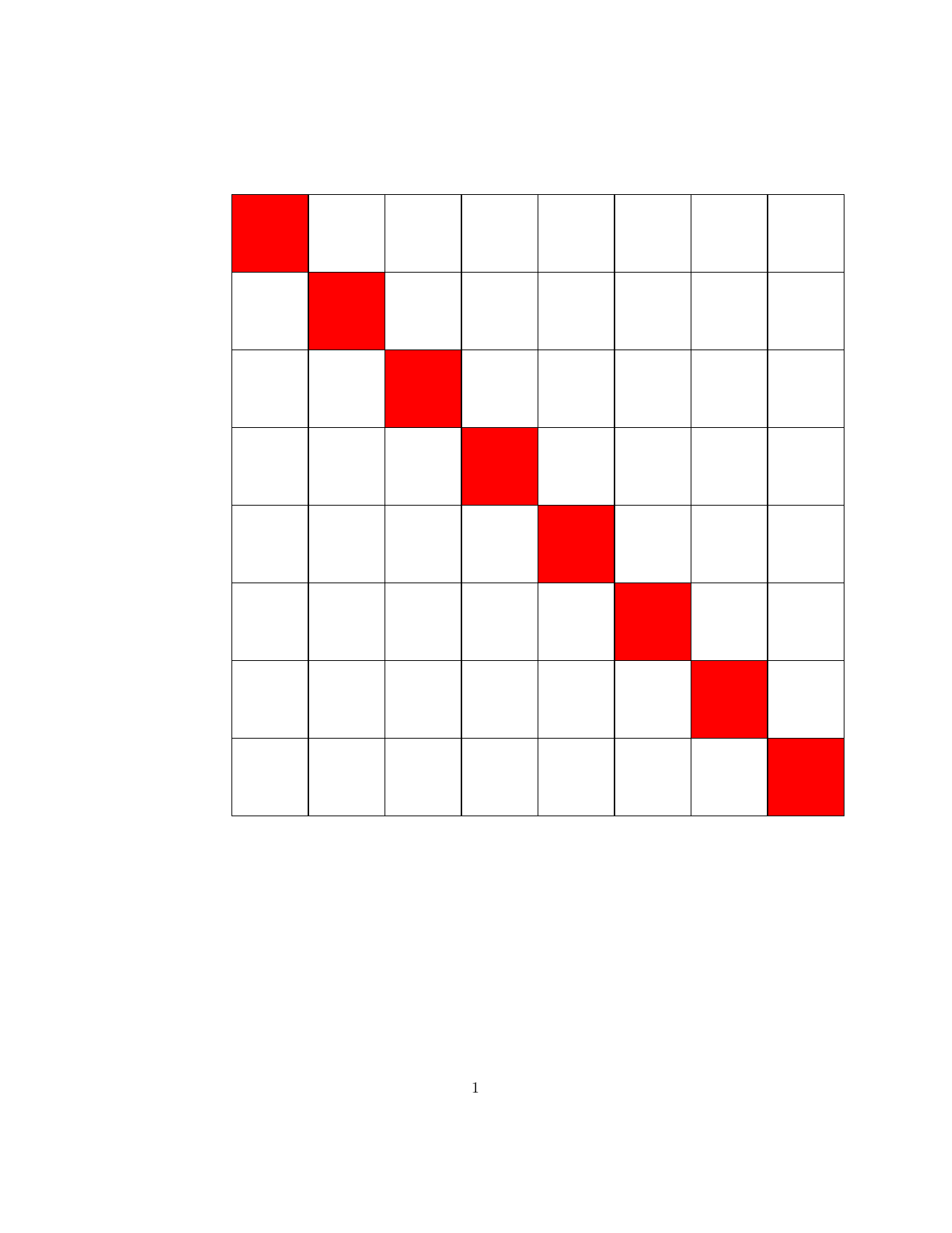
Well-known (group) structures in matrix $\mathbf{B}$ are illustrated in the following figure.

Dense (invertible) Triangular (Cholesky) Diagonal (invertible)

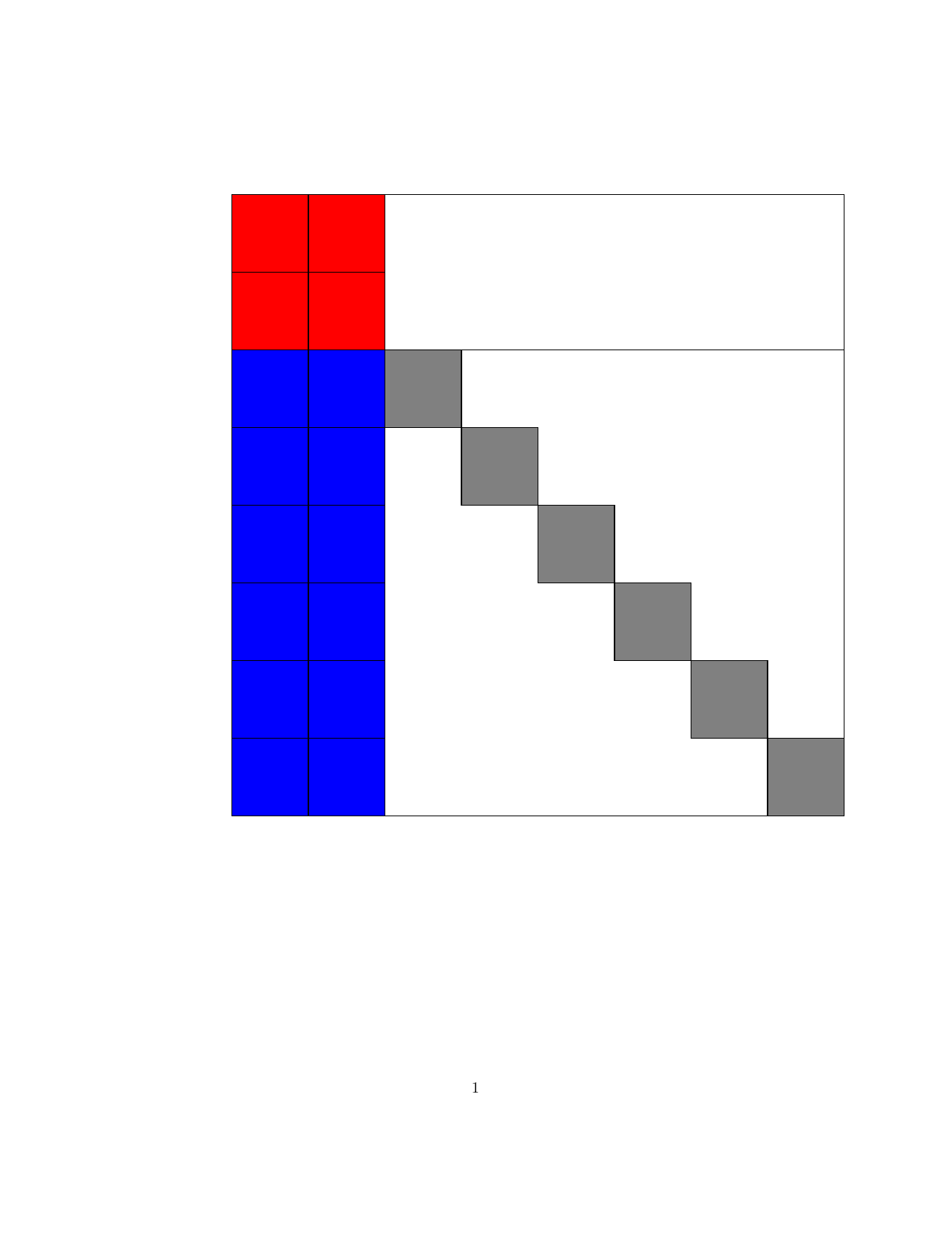
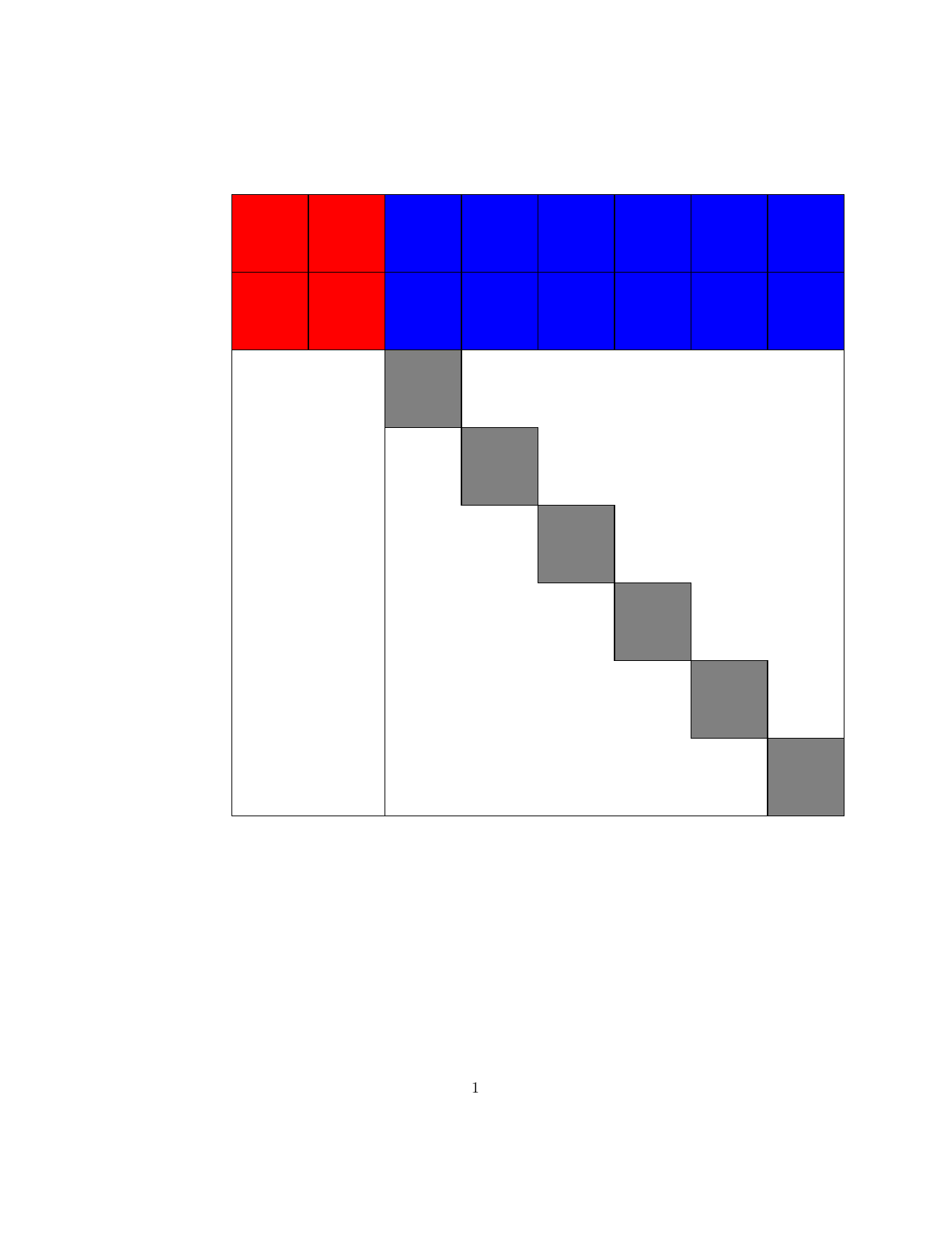
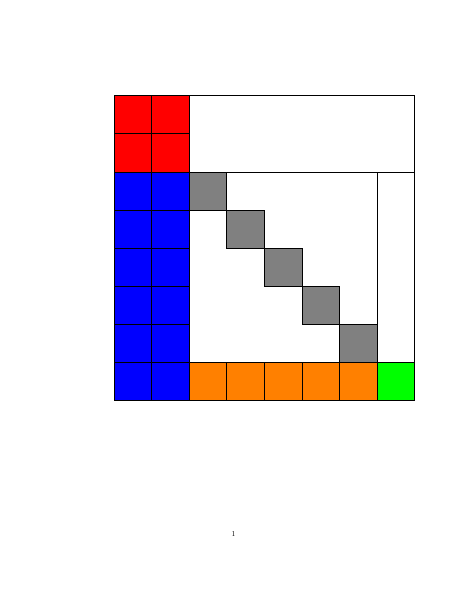
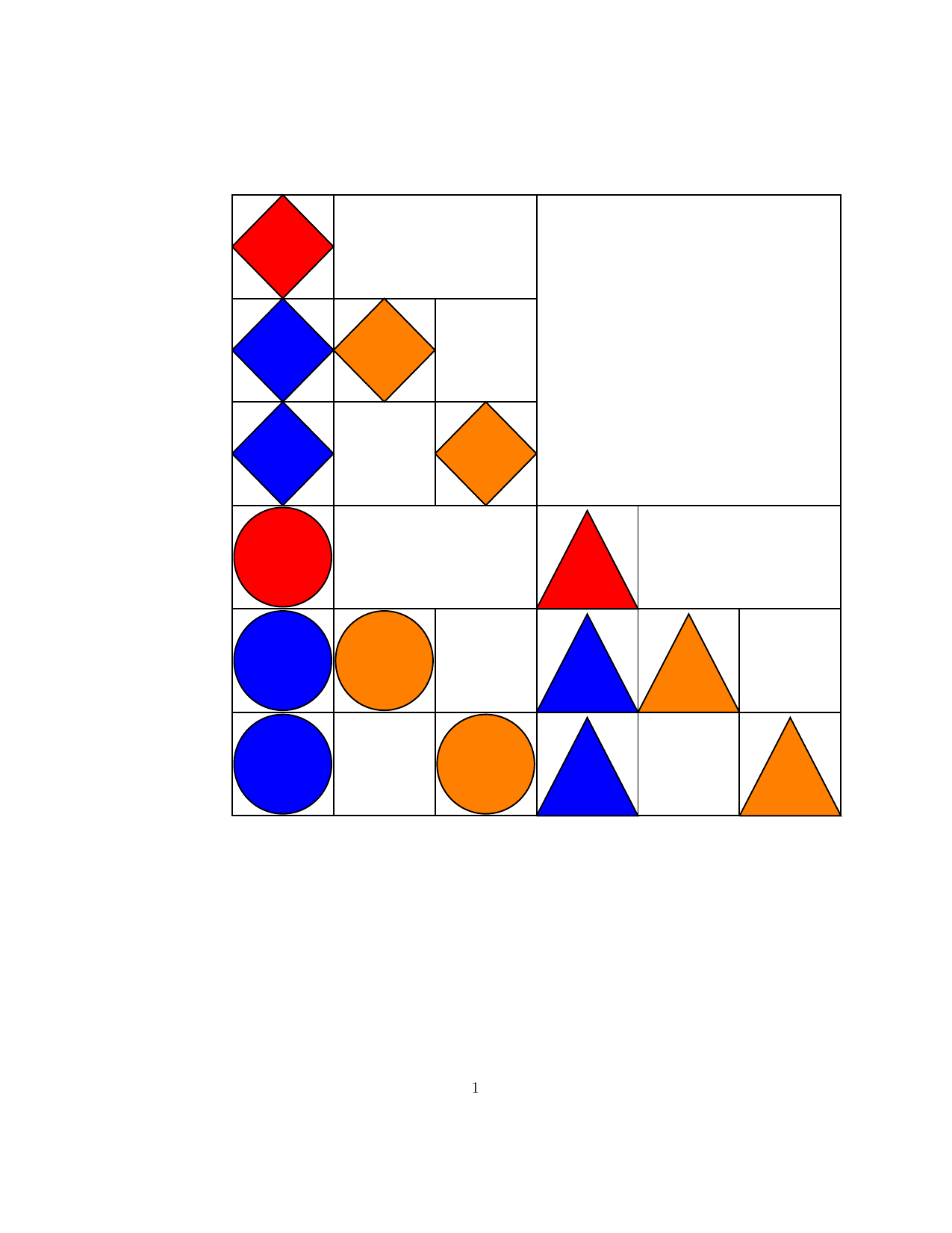
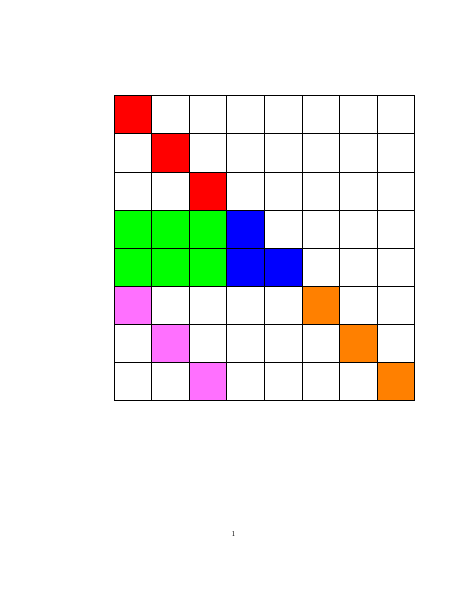
Structured Gaussian with Flexible Precision

Structures in precision $\mathbf{S}$, where $\mathbf{S}=\mathbf{B}\mathbf{B}^T$ and matrix $\mathbf{B}$ is a sparse (group) member as below.

Block lower
triangular		 Block upper
triangular		 Hierarchical
(lower Heisenberg)		 Kronecker product Triangular-Toeplitz Sparse Cholesky
$\begin{bmatrix} \mathbf{B}_A & \mathbf{0} \\ \mathbf{B}_C & \mathbf{B}_D \end{bmatrix}$ $\begin{bmatrix} \mathbf{B}_A & \mathbf{B}_B \\ \mathbf{0} & \mathbf{B}_D \end{bmatrix}$ $\begin{bmatrix} \mathbf{B}_A & \mathbf{0} \\ \mathbf{B}_C & \begin{bmatrix} \mathbf{B}_{D_1} & \mathbf{0} \\ \mathbf{B}_{3} & \mathbf{B}_{4} \end{bmatrix} \end{bmatrix}$ $\begin{bmatrix} d & 0 \\ s & t \end{bmatrix} \otimes \begin{bmatrix} r & 0 & 0 \\ {b}_1 & {o}_1 & 0 \\ {b}_2 & 0 & {o}_2 \end{bmatrix} $ $\begin{bmatrix} r & 0 & 0 &0 \\ y & r & 0 & 0 \\ g & y & r & 0 \\ b & g & y & r \end{bmatrix}$ $\begin{bmatrix} \mathbf{B}_{D_1} & \mathbf{0} & \mathbf{0} \\ \mathbf{B}_{A} & \mathbf{B}_{B} & \mathbf{0} \\ \mathbf{B}_{D_2} & \mathbf{0} & \mathbf{B}_{D_3} \end{bmatrix}$

A Structured Gaussian Example:

Auxiliary parameter $\mathbf{B}$ lives in a structured space (matrix Lie group): ${\cal{B}_{\text{up}}}(k)$, a block upper-triangular sub-group of $\mathrm{GL}^{p \times p}$;

$$ \begin{aligned} {\cal{B}_{\text{up}}}(k) := \Big\{ \begin{bmatrix} \mathbf{B}_A & \mathbf{B}_B \\ \mathbf{0} & \mathbf{B}_D \end{bmatrix} \Big| & \mathbf{B}_A \in \mathrm{GL}^{k \times k},\, \mathbf{B}_D \in{\cal D}^{(p-k) \times (p-k)}_{++} \Big\},\,\, \end{aligned} $$

When $k=0$, the space ${\cal{B}_{\text{up}}}(0) = {\cal D}^{p \times p}_{++}$ becomes the diagonal case. When $k=p$, ${\cal{B}_{\text{up}}}(p) = \mathrm{GL}^{p\times p}$ becomes the dense case.

Consider a local parameter space (sub-space of Lie algebra): ${\cal{M}_{\text{up}}}(k)$.

$$ \begin{aligned} {\cal{M}_{\text{up}}}(k): = \Big\{ \begin{bmatrix} \mathbf{M}_A & \mathbf{M}_B \\ \mathbf{0} & \mathbf{M}_D \end{bmatrix} \Big| & \mathbf{M}_A \in{\cal S}^{k \times k}, \, \mathbf{M}_D \in{\cal D}^{(p-k) \times (p-k)} \Big\} \end{aligned} $$

The global, auxiliary, and local parameterizations : $$ \begin{aligned} \tau &= \Big\{\mu \in \mathcal{R}^p, \mathbf{S}=\mathbf{B} \mathbf{B}^T \in \mathcal{S}_{++}^{p\times p} | \mathbf{B} \in {\cal{B}_{\text{up}}}(k) \Big\}, \\ \lambda & = \Big\{ \mu \in \mathcal{R}^p, \mathbf{B} \in {\cal{B}_{\text{up}}}(k) \Big\},\\ \eta &= \Big\{ \delta\in \mathcal{R}^p, \mathbf{M} \in {\cal{M}_{\text{up}}}(k) \Big\}. \end{aligned} $$

Maps $\psi$ and $\phi_{\lambda_t}$ are defined in $\eqref{3}$. Our NGD update in the auxiliary space is shown below, where we assume $\eta_0=\mathbf{0}$.

Structure-preserving update in $\lambda$ space

$$ \begin{aligned} \Big\{ \begin{array}{c} \mu_{t+1} \\ \mathbf{B}_{t+1} \end{array} \Big\} = \lambda_{t+1} = \phi_{\lambda_t} \big( \eta_0-\beta \hat{\mathbf{g}}_{\eta_0}^{(t)} \big) =\Big\{ \begin{array}{c} \mu_t - \beta \mathbf{B}_{t}^{-T} \mathbf{B}_t^{-1} \mathbf{g}_{\mu_t} \\ \mathbf{B}_t \mathbf{h} \Big( \beta \mathbf{C}_{\text{up}} \odot \kappa_{\text{up}}\big( 2 \mathbf{B}_t^{-1} \mathbf{g}_{\Sigma_t} \mathbf{B}_t^{-T} \big) \Big) \end{array} \Big\} \end{aligned} $$

where $\odot$ is the elementwise product , $\kappa_{\text{up}}(\mathbf{X}) \in {\cal{M}_{\text{up}}}(k)$ extracts non-zero entries of ${\cal{M}_{\text{up}}}(k)$ from $\mathbf{X}$, $ \mathbf{C}_{\text{up}} = \begin{bmatrix} \frac{1}{2} \mathbf{J}_A & \mathbf{J}_B \\ \mathbf{0} & \frac{1}{2} \mathbf{I}_D \end{bmatrix} \in {\cal{M}_{\text{up}}}(k)$, and $\mathbf{J}$ is a matrix of ones.

Note that (see [1] for the detail)

  • $ \mathbf{B}_{t+1} \in$ matrix Lie group ${\cal{B}_{\text{up}}}(k)$ since $$ \begin{aligned} &\mathbf{h}\big(\mathbf{M}\big) \in {\cal{B}_{\text{up}}}(k) \text{ for } \mathbf{M} \in \text{Lie algebra of } {\cal{B}_{\text{up}}}(k) \,\,\,\, &(\text{by design, } \mathbf{h}(\cdot) \text{ is a Lie-group retraction}) \\ &\mathbf{B}_{t} \in {\cal{B}_{\text{up}}}(k) \,\,\,\, & (\text{by construction}) \\ &\mathbf{B}_{t+1} = \mathbf{B}_{t}\mathbf{h}\big(\mathbf{M}\big) \,\,\,\, & (\text{closed under the group product}) \end{aligned} $$
  • $\mathbf{B}$ also induces a low-rank-plus-diagonal structure in covariance matrix $\Sigma=\mathbf{S}^{-1}$, where $\mathbf{S}=\mathbf{B}\mathbf{B}^T$.

In summary, our NGD method:

  • is a systematic approach to incorporate structures
  • induces exact and non-singular FIMs

Applications

Structured 2nd-order Methods for Non-convex Optimization

Given an optimization problem $$ \begin{aligned} \min_{\mu \in \mathcal{R}^p} \ell(\mu), \end{aligned}\tag{5}\label{5} $$

we formulate a new problem over Gaussian $q(\mathbf{w}|\tau)$ with structured precision, which is a special case of $\eqref{1}$ with $\gamma=1$. $$ \begin{aligned} \min_{\tau \in \Omega_\tau} E_{q(w|\tau)} \big[ \ell(\mathbf{w}) \big] + E_{q(w|\tau)} \big[ \log q(\mathbf{w}|\tau)\big], \end{aligned}\tag{6}\label{6} $$ where $\mathbf{B} \in {\cal{B}_{\text{up}}}(k)$ is a block upper-triangular group member, $\tau=(\mu,\mathbf{S})$ with mean $\mu$ and precision matrix $\mathbf{S}=\mathbf{B}\mathbf{B}^T$.

Using our NGD to solve $\eqref{6}$

  • gives the following update $$ \begin{aligned} \mu_{t+1} & \leftarrow \mu_{t} - \beta \mathbf{S}_t^{-1} \mathbf{g}_{\mu_t},\\ \mathbf{B}_{t+1} & \leftarrow \mathbf{B}_t \mathbf{h} \Big( \beta \mathbf{C}_{\text{up}} \odot \kappa_{\text{up}}\big( 2 \mathbf{B}_t^{-1} \mathbf{g}_{\Sigma_t} \mathbf{B}_t^{-T} \big) \Big) \end{aligned} $$
  • obtains an update to solve $\eqref{5}$ with group-structural invariance [4]: $$ \begin{aligned} \mu_{t+1} & \leftarrow \mu_t - \beta \mathbf{S}_{t}^{-1} \nabla_{\mu_t} \ell( \mu), \\ \mathbf{B}_{t+1} & \leftarrow \mathbf{B}_t \mathbf{h} \Big( \beta \mathbf{C}_{\text{up}} \odot { \color{red}\kappa_{\text{up}}\big( \mathbf{B}_t^{-1} \nabla_{\mu_t}^2 \ell( \mu) \mathbf{B}_t^{-T} - \mathbf{I} \big)} \Big) \end{aligned}\tag{7}\label{7} $$ by using $\eqref{4}$ evaluated at the mean $\mu_t$ $$ \begin{aligned} \mathbf{g}_{\mu_t} \approx \nabla_{\mu_t} \ell( \mu),\,\,\,\, \mathbf{g}_{\Sigma_t} \approx \frac{1}{2} \big[ \nabla_{\mu_t}^2 \ell( \mu) - \mathbf{S}_t\big]. \end{aligned}\tag{8}\label{8} $$ where $\Sigma=\mathbf{S}^{-1}$ is the covariance.
Group-structural invariance: (Click to expand)

Recall that $\mathbf{B} \in {\cal{B}_{\text{up}}}(k)$. The update in $\eqref{7}$ is invariant under any (group) transform $\mathbf{R}^T \in {\cal{B}_{\text{up}}}(k)$ of $\eqref{5}$ such as $\min_{y \in \mathcal{R}^p} \ell(\mathbf{R} \, \mathbf{y})$.

Time complexity: (Click to expand)
  • $O(k^2 p)$ for triangular structure,
  • $O( (k_1^2+k_2^2) p)$ for hierarchical structure.

Implementation using Hessian-vector products (HVPs);

  • Off-diagonal: $k$ HVPs (triangular), $(k_1+k_2)$ HVPs (hierarchical),
  • Diagonal: compute/approximate diagonal entries of $\nabla_{\mu_t}^2 \ell( \mu)$.
Classical non-convex optimization: (Click to expand)
200-dim non-separable, non-convex functions
Performance of our method with group structures (lower-triangular, upper-triangular, upper Heisenberg, lower Heisenberg), Adam, and BFGS

Structured Adaptive-gradient Methods for Deep Learning

At each NN layer, consider a Gaussian family $q(\mathbf{w}|\mu,\mathbf{S})$ with a Kronecker product structure, where $\tau=(\mu,\mathbf{S})$.

Our method gives adaptive-gradient updates with group-structural invariance by approximating $\nabla_{\mu_t}^2 \ell( \mu)$ in $\eqref{8}$ using the Gauss-Newton.

The Kronecker product ($\mathbf{B}=\mathbf{B}_1 \otimes \mathbf{B}_2$) of two sparse structured groups ($\mathbf{B} _1$ and $\mathbf{B}_2$) further reduces the time complexity, where precision $\mathbf{S}=\mathbf{B}\mathbf{B}^T= (\mathbf{B}_1 \mathbf{B}_1^T) \otimes (\mathbf{B}_2 \mathbf{B}_2^T)$

Time complexity: (Click to expand)
  • $O(k p)$ for our Kronecker product with triangular groups, where $0<k<p^{1/2}$
  • $O( (k_1+k_2) p)$ for our Kronecker product with hierarchical groups, where $0<k_1+k_2<p^{1/2}$
  • $O(p)$ for Adam and our diagonal groups
  • $O(p^{3/2})$ for KFAC and our Kronecker product with dense groups

Implementation:

  • Automatically parallelized by Auto-Differentiation
  • No sequential conjugate-gradient (CG) steps
Image classification problems: (Click to expand)
Kronecker product of lower-triangular groups for CNN
Comparison between our method with Kronecker product groups and Adam

Variational Inference with Gaussian Mixtures

Our NGD

  • can use structured Gaussian mixtures as flexible variational distributions: $q(\mathbf{w}|\tau)=\frac{1}{C}\sum_{c=1}^{C}q(\mathbf{w}|\mu_c,\mathbf{S}_c)$
  • gives efficient stochastic natural-gradient variational methods beyond mean-field/diagonal covariance
Approximating 80-dim multimodal distributions: (Click to expand)
First 8 marginal distributions of Gaussian mixture approximation with upper-triangular structure
Comparison between our approximation ($k=5$) and the ground-truth (mixture of t distributions)

References

[1] W. Lin, F. Nielsen, M. E. Khan, & M. Schmidt, "Tractable structured natural gradient descent using local parameterizations," International Conference on Machine Learning (ICML) (2021).

[2] M. Opper & C. Archambeau, "The variational Gaussian approximation revisited," Neural computation 21:786–792 (2009).

[3] T. Glasmachers, T. Schaul, S. Yi, D. Wierstra, & J. Schmidhuber, "Exponential natural evolution strategies," Proceedings of the 12th annual conference on Genetic and evolutionary computation (2010), pp. 393–400.

[4] W. Lin, F. Nielsen, M. E. Khan, & M. Schmidt, "Structured second-order methods via natural gradient descent," arXiv preprint arXiv:2107.10884 (2021).

[5] W. Lin, M. E. Khan, & M. Schmidt, "Stein’s Lemma for the Reparameterization Trick with Exponential Family Mixtures," arXiv preprint arXiv:1910.13398 (2019).

[6] W. Lin, M. Schmidt, & M. E. Khan, "Handling the positive-definite constraint in the bayesian learning rule," International Conference on Machine Learning (PMLR, 2020), pp. 6116–6126.

You may also enjoy

Part III: Invariance of Natural-Gradients

14 minute read

Goal (edited: 01-Jan-23) This blog post focuses on invariant properties of natural-gradients. We will discuss transformation rules of natural-gradients, ...