Part IV: Natural Gradient Descent and its Extension—Riemannian Gradient Descent
Warning: working in Progress (incomplete)
Goal (edited: 07-Jan-23)
This blog post should help readers to understand natural-gradient descent and Riemannian gradient descent. We also discuss some invariance property of natural-gradient descent, Riemannian gradient descent, and Newton’s method.
We will give an informal introduction with a focus on high level of ideas.
Click to see how to cite this blog post
Two kinds of Spaces
We will discuss (Riemannian) gradient spaces and parameter spaces for gradient-based updates.
As we disucssed in Part II, the parameter space $\Omega_\tau$ and the tangent space denoted by $T_{\tau_0}\mathcal{M}$ at point $\tau_0$ are two distinct spaces.
Given intrinsic parametrization $\tau$, the tangent space is a (complete) vector space and $T_{\tau_0}\mathcal{M}=\mathcal{R}^K$ while the parameter space $\Omega_\tau$ is like a local vector space in $\mathcal{R}^K$, where $K$ is the dimension of the manifold. In other words, $\Omega_\tau$ is often an open (proper) subset of $\mathcal{R}^K$.
In manifold cases, we have to explicitly distinguish the difference between the representation of a point (parameter) and a vector (Riemannian gradient). These two spaces are different in many aspects such as the domain and the distance. Mathematically speaking, a (Riemannian) gradient space is much simpler and nicer than a parameter space.
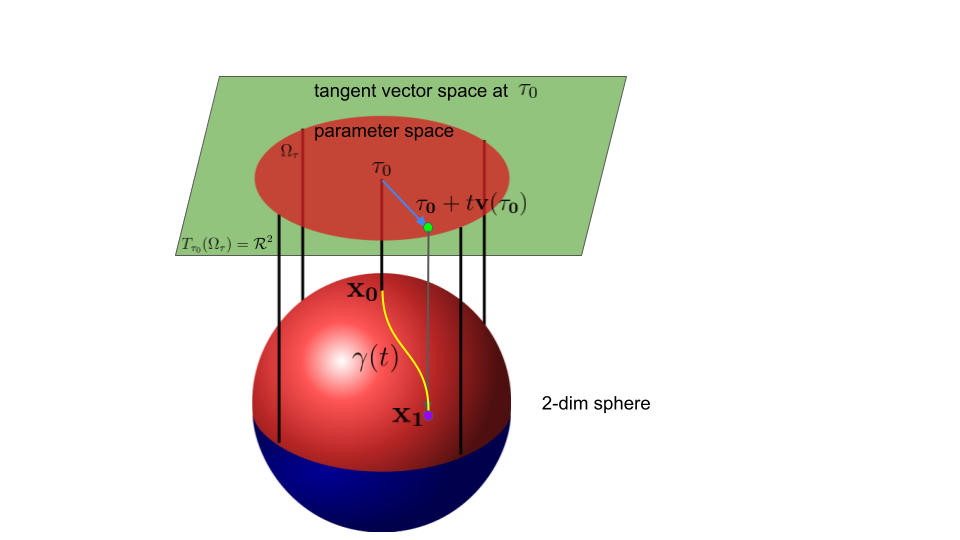
Natural-gradient Descent in an Intrinsic Parameter Space
Using intrinsic parametrization $\tau$, we can perform a natural-gradient update known as natural-gradient descent (NGD) [1] when we use the Fisher-Rao metric.
$$
\begin{aligned}
\mathrm{NGD:} &\,\,\,\,\,
\tau_{k+1} \leftarrow \tau_{k} - \alpha \hat{\mathbf{g}}_{\tau_k}
\end{aligned}\tag{1}\label{1}
$$
where $\hat{\mathbf{g}}_{\tau_k}:=-\mathbf{v}(\tau_k) $ is a natural gradient evaluated at point $\tau_{k}$ and $\alpha:=t>0$ is a step-size.
This update in Eq. $\eqref{1}$ is inspired by the standard linear update in the tangent vector space (see the green space in the above figure).
By choosing an intrinsic parametrization, this update is also valid in the parameter space1 (see the red space in the above figure) as long as the step-size is small
enough.
The update in the parameter space is valid since the parameter space $\Omega_\tau$ has a local vector-space structure thanks to the use of an intrinsic parametrization.
However, when $\Omega_\tau$ is a proper subset of $T_{\tau_k}\mathcal{M}$ (i.e., $\Omega_\tau \neq T_{\tau_k}\mathcal{M} $), the update in Eq. $\eqref{1}$ is valid only when the step-size $\alpha$ is small enough so that $\tau_{k+1} \in \Omega_\tau$.
Warning:
Using a small step-size could be an issue since it could greatly slow down the progression of natural-gradient descent in practice.
Example of NGD in a constrained space: (click to expand)
Natural-gradient Descent is Linearly Invariant
Recall that in Part III, we have shown that natural gradients are invariant under any intrinsic parameter transformation. The parameter transformation can be non-linear.
It is natural to expect that natural-gradient descent has a similar property. Unfortunately, natural-gradient descent is only invariant under an intrinsic linear transformation. Note that Newton’s method is also linearly invariant while Euclidean gradient descent is not.
Let’s consider the following (scalar) optimization problem on a smooth manifold $\mathcal{M}$ with the Fisher-Rao metric $F$.
$$
\begin{aligned}
\min_{x \in \mathcal{M}} h(x)
\end{aligned}\tag{2}\label{2}
$$
Note that $\mathcal{M}$ in general does not have a vector-space structure.
We has to artificially choose an intrinsic parameterization $\tau$ so that the parameter space $\Omega_\tau$ at least has a local vector-space structure.
The problem in $\eqref{2}$ can be re-expressed as below.
$$
\begin{aligned}
\min_{\tau \in \Omega_\tau} h_\tau(\tau)
\end{aligned}
$$ where $h_\tau$ is the parameter representation of the smooth function $h$.
Natural gradient descent in this parameter space $\Omega_\tau$ is
$$
\begin{aligned}
\tau_{k+1} \leftarrow \tau_{k} - \alpha \hat{\mathbf{g}}_{\tau_k}
\end{aligned}\tag{3}\label{3}
$$ where $\mathbf{F}_\lambda$ is the FIM, natural gradient is $\hat{\mathbf{g}}_{\tau_k} := [\mathbf{F}_\tau(\tau_k) ]^{-1} \nabla_\tau h_\tau(\tau_k)$ and the step-size $\alpha$ is small enough so that $\tau_{k+1} \in \Omega_\tau$.
Consider another intrinsic parameterization $\lambda$ so that $\lambda=\mathbf{U} \tau$, where $\mathbf{U}$ is a constant (square) invertible matrix.
For simplicity, we further assume $\Omega_\lambda=\{ \mathbf{U}\tau |\tau \in\Omega_\tau \} $, where $\Omega_\lambda$ is the parameter space of $\lambda$.
Natural gradient descent in this parameter space $\Omega_\lambda$ is
$$
\begin{aligned}
\lambda_{k+1} \leftarrow \lambda_{k} - \alpha \hat{\mathbf{g}}_{\lambda_k}
\end{aligned}\tag{4}\label{4}
$$ where $\hat{\mathbf{g}}_{\lambda_k} := [\mathbf{F}_\lambda(\lambda_k) ]^{-1} \nabla_\lambda h_\lambda(\lambda_k)$ and the cost function is $h_\lambda(\lambda) = h_\tau(\tau(\lambda))$.
Recall that we have the transformation rule for natural gradients as
$$
\begin{aligned}
\hat{\mathbf{g}}_\tau= \mathbf{Q} \hat{\mathbf{g}}_\lambda
\end{aligned}
$$ where $Q_{ji}=\frac{\partial \tau^j(\lambda)}{\partial \lambda^i}$.
We can verify that $\mathbf{Q} = \mathbf{U}^{-1}$. Notice that $\tau_0 = \mathbf{U}^{-1} \lambda_0$ by construction.
The update in $\eqref{3}$ at iteration $k=1$ then can be re-expressed as
$$
\begin{aligned}
\tau_{1} \leftarrow \tau_{0} - \alpha \hat{\mathbf{g}}_{\tau_0} = \mathbf{U}^{-1} \lambda_0 - \alpha \mathbf{U}^{-1} \hat{\mathbf{g}}_{\lambda_0} = \mathbf{U}^{-1} \lambda_1
\end{aligned}
$$
When $\alpha$ is small enough, we have $\tau_1 \in \Omega_\tau$ and $\lambda_1 \in \Omega_\lambda$.
It is easy to show that $\tau_k = \mathbf{U}^{-1} \lambda_k$ by induction.
Therefore, updates in $\eqref{3}$ and $\eqref{4}$ are equivalent.
Riemannian Gradient Descent and its (Non-linear) Invariance
Now we discuss a gradient-based method that is invariant to any intrinsic parameter transformation.
As mentioned before, a manifold in general does not have a vector-space structure.
We has to artificially choose an intrinsic parameterization $\tau$, which gives rise to
a parametrization-dependence.
Therefore, it will be ideal if a
gradient-based method does not dependent on the choice of intrinsic parametrizations.
We will first introduce the concept of a (one-dimensional) geodesic $\gamma(t)$, which is the “shortest curve” on a manifold with a Riemannian metric (i.e., the Fisher-Rao metric). Recall that in Part II we only define a distance between two Riemannian gradients evaluated at the same point. We can use the length of the shortest geodesic to define the distance between two points on the manifold. In statistics, the distance induced by a geodesic with the Fisher-Rao metric is known as the Rao distance [2]. This is known as the boundary value problem (BVP) of a geodesic. The boundary conditions are specified by a starting point and an end point on the manifold. To solve this problem, we often solve an easier problem, which is known as the initial value problem (IVP) of a geodesic. The initial conditions are specified by a starting point and an initial Riemannian gradient/velocity.
We will only consider the IVP of a geodesic for simplicity.
Consider an intrinsic parametrization $\tau$, where $\gamma_\tau(t)$ is the parameter representation of the geodesic.
To specify a geodesic, we need to provide a starting point $\tau_0$ on the manifold and a Riemannian gradient $\mathbf{v}_{\tau_0}$ evluated at point $\tau_0$.
The geodesic is the solution of a system of second-order non-linear ordinary differential equations (ODE) with the following initial conditions.
$$
\begin{aligned}
\gamma_\tau(0) = \tau_0; \,\,\,\,\,\,
\frac{d \gamma_\tau(t) }{d t} \Big|_{t=0} = \mathbf{v}_{\tau_0}
\end{aligned}
$$ where the geodesic is uniquely determined by the initial conditions and $\mathbf{I}_\tau$ is the domain of the parametric geodesic curve. We assume 0 is contained in the domain for simplicity.
For a geodesically complete manifold, the domain of the geodesic is the whole space $\mathbf{I}_{\tau}
=\mathcal{R}$. We will only consider this case in this post.
To avoid explicitly writing down the differential equations of a geodesic2 (i.e., Christoffel symbols or connection 1-form in a section),
researchers refer to it as the manifold exponential map.
Given an intrinsic parametrization $\tau$,
the map at point $\tau_0$ is defined as
$$
\begin{aligned}
\mathrm{Exp}_{\tau_0}\colon T_{\tau_0}\mathcal{M} & \mapsto \mathcal{M}\\
\mathbf{v}_{\tau_0} & \mapsto \gamma_\tau(1) \,\,\,\, \textrm{s.t.} \,\,\,\,\,\, \gamma_\tau(0) = \tau_0;\,\,\,\,\,\,
\frac{d \gamma_\tau(t) }{d t} \Big|_{t=0} = \mathbf{v}_{\tau_0}
\end{aligned}
$$ where $t$ is fixed to be 1 and $\tau_0$ denotes the initial point under parametrization $\tau$.
Warning:
The exponential map is a geometric object. We use a parametric representation of a geodesic curve to define the exponential map. Thus, the form/expression of the map does depend on the choice of parametrizations.
Now, we can define a Riemannian gradient method.
Under intrinsic parametrization $\tau$ of a manifold, (exact) Riemannian gradient descent (RGD) is defined as
$$
\begin{aligned}
\mathrm{RGD:} &\,\,\,\,\,
\tau_{k+1} \leftarrow \mathrm{Exp}_{\tau_k} (- \alpha \hat{\mathbf{g}}_{\tau_k} )
\end{aligned}
$$
where $\tau_{k+1}$ always stays on the manifold thanks to the exponential map since $\hat{\mathbf{g}}_{\tau_k}$ is in the domain of the exponential map.
The invariance of this update is due to the uniqueness of the geodesic and the invariance of the Euler-Lagrange equation. We will not discuss this further in this post to avoid complicated derivations. We will cover this in future posts about calculus of variations.
Although Riemannian gradient descent is nice, the exponential map or the geodesic often has a high computational cost and does not admit a closed-form expression.
Many faces of Natural-gradient Descent
Natural-gradient Descent as Inexact Riemannian Gradient Descent
Natural-gradient descent can be derived from a first-order (linear) approximation of the geodesic, which implies that natural-gradient descent is indeed an inexact Riemannian gradient update. Natural-gradient descent is linearly invariant due to the approximation.
Consider a first-order Taylor approximation at $t=0$ of the geodesic shown below.
$$
\begin{aligned}
\gamma_\tau(t) \approx \gamma_\tau(0) + \frac{d \gamma_\tau(t)}{d t} \Big|_{t=0} (t-0)
\end{aligned}
$$
Warning:
This approximation does not guarantee that the approximated geodesic stays on the manifold for all $t \neq 0$.
Recall that the exponential map is defined via the geodesic $\gamma_\tau(1)$.
We can use this approximation of the geodesic to define a new map (A.K.A. the Euclidean retraction map) as shown below.
$$
\begin{aligned}
\mathrm{Ret}_{\tau_0}(\mathbf{v}_{\tau_0}) := \gamma_\tau(0) + \frac{d \gamma_\tau(t)}{d t} \Big|_{t=0} (1-0) =\tau_0 + \mathbf{v}_{\tau_0}
\end{aligned}
$$
Therefore, an inexact Riemannian gradient update with this new map is defined as
$$
\begin{aligned}
\tau_{k+1} \leftarrow \mathrm{Ret}_{\tau_k} (- \alpha \hat{\mathbf{g}}_{\tau_k} ) = \tau_k - \alpha \hat{\mathbf{g}}_{\tau_k}
\end{aligned}
$$ which recovers natural-gradient descent.
Natural-gradient Descent as Unconstrained Proximal-gradient Descent
In this section, we will make an additional assumption:
Additional assumption:
The parameter space $\Omega_\tau=\mathcal{R}^K$ is unconstrained.
As we mentioned before, the distances in the gradient space and the parameter space are defined differently. In the previous section, we use the geodesic to define the distance between two points in a parameter space.
We could also use other “distances” denoted by $\mathrm{D}(.,.)$ (i.e., Kullback–Leibler divergence) [3] to define the length between two points in a parameter space.
In the following section, we assume $p(w|\mathbf{y})$ and $p(w|\tau_k)$ are two members in a parameteric distribution family $p(w|\tau)$ indexed by $\mathbf{y}$ and $\tau_k$, respectively.
We define a class of f-divergence in this case. Note that a f-divergence can be defined in a more general setting.
Csiszar f-divergence
Let $f:(0,+\infty)\mapsto \mathcal{R}$ be a smooth scalar function satisfying all the following conditions.
- convex in its domain
$f(1)=0$$\ddot{f}(1)=1$
A f-divergence for a parametric family $p(w|\tau)$ is defined as
$$
\begin{aligned}
\mathrm{D}_f(\mathbf{y},\tau_k) := \int f(\frac{p(w|\mathbf{y})}{p(w|\tau_k)}) p(w|\tau_k) dw.
\end{aligned}
$$
Thanks to Jensen’s inequality,
a f-divergence is always non-negative as
$$
\begin{aligned}
\mathrm{D}_f(\mathbf{y},\tau_k) \geq f( \int \frac{p(w|\mathbf{y})}{p(w|\tau_k)} p(w|\tau_k) dw ) = f(\int p(w|\mathbf{y})dw) =f(1) =0 .
\end{aligned}
$$
The KL divergence is a f-divergence where $f(t)=-\log(t)$.
Proximal-gradient descent
Given such a “distance” $\mathrm{D}(\mathbf{y},\tau_k)$, we could perform an unconstrained proximal-gradient update as
$$
\begin{aligned}
\tau_{k+1} \leftarrow \arg\min_{\mathbf{y} \in \mathcal{R}^K } \{ \langle \mathbf{g}_{\tau_k}, \mathbf{y}\rangle + \frac{1}{\alpha} \mathrm{D}(\mathbf{y},\tau_k) \}
\end{aligned}
$$ where $\mathbf{g}_{\tau_k}$ is a Eulcidean gradient and the parameter space $\Omega_\tau$ is unconstrained.
Claim:
The secord-order Taylor approximation of any f-divergence $\mathrm{D}_f(\mathbf{y},\tau_k)$ at $\mathbf{y}=\tau_k$ is $\frac{1}{2}(\mathbf{y}-\tau_k)^T \mathbf{F}_\tau(\tau_k) (\mathbf{y}-\tau_k)$
Proof of the claim: (click to expand)
By the claim, when $\mathrm{D}(\mathbf{y},\tau_k)$ is the second-order Taylor approximation of a
f-divergence $\mathrm{D}_f(\mathbf{y},\tau_k)$ at $\mathbf{y}=\tau_k$,
the unconstrained proximal-gradient update can be re-expressed as
$$
\begin{aligned}
\tau_{k+1} \leftarrow \arg\min_{y \in \mathcal{R}^K } \{ \langle \mathbf{g}_{\tau_k}, \mathbf{y} \rangle + \frac{1}{2\alpha} (\mathbf{y}-\tau_k)^T \mathbf{F}_\tau(\tau_k) (\mathbf{y}-\tau_k) \}
\end{aligned}
$$
It is easy to see that we can obtain the following natural-gradient update from the above expression.
$$
\begin{aligned}
\tau_{k+1} \leftarrow \tau_{k} - \alpha \underbrace{ \mathbf{F}^{-1}_\tau(\tau_k) \mathbf{g}_{\tau_k}}_{ =\hat{\mathbf{g}}_{\tau_k} }
\end{aligned}
$$
Note
The Taylor expansion
- uses the distance defined in a (Riemannian) gradient space to approximate the distance in a parameter space.
- implicitly assumes that the parameter space
$\Omega_\tau$is open due to the definition of the expansion.
In Part V , we will show that $\mathrm{D}(y,\tau_k)$ can also be an exact KL divergence when $p(w)$ is an exponential family.
Under a particular parametrization, natural-gradient descent also can be viewed as (unconstrained) mirror descent.
Warning:
The connection bewteen natural-gradient descent and proximal-gradient/mirror descent could break down in constrained cases unless $\alpha$ is small enough. We will cover more about this point in Part VI.
Natural-gradient Descent in Non-intrinsic Parameter Spaces
As mentioned in Part I, an intrinsic parametrization creates a nice parameter space (e.g., a local vector space structure) and guarantees a non-singular FIM. We now discuss issues when it comes to natural-gradient descent over non-intrinsic parametrizations including overparameterization.
-
We may not have a local vector space structure in a non-intrinsic parameter space. Therefore, natural-gradient descent in this parameter space is pointless since the updated parameter will leave the parameter space. Indeed, the FIM could also be ill-defined in such cases. We will illustrate this by examples.
Bernoulli Example: Invalid NGD (click to expand)
Von Mises–Fisher Example: Invalid NGD (click to expand)
- The FIM is singular in a non-intrinsic space. In theory, Moore–Penrose inverse could be used to compute natural-gradients so that natural-gradient descent is linearly invariant in this case. However, Moore–Penrose inverse often has to use the singular value decomposition (SVD) and destroies structures of the FIM. In practice, the iteration cost of Moore–Penrose inverse is very high as illustrated in the following example.
Example: High iteration cost (click to expand)
- It is tempting to approximate the singular FIM by an emprical FIM with a scalar damping term and use Woodbury matrix identity to reduce the iteration cost of computing natural-gradients. However, sample-based emprical approximations could be problematic [4]. Moreover, damping introduces an additional tuning hyper-parameter and destories the linear invariance property of natural-gradient descent. Such an approximation should be used with caution.
Euclidean Gradient Descent is NOT (Linearly) Invariant
For simplicity, consider an unconstrained optimization problem.
$$
\begin{aligned}
\min_{\tau \in \mathcal{R}^K } h_\tau(\tau)
\end{aligned}
$$
Euclidean gradient descent (GD) in parametrization $\tau$ is
$$
\begin{aligned}
\tau_{k+1} \leftarrow \tau_{k} - \alpha {\mathbf{g}}_{\tau_k}
\end{aligned}\tag{5}\label{5}
$$ where ${\mathbf{g}}_{\tau_k} := \nabla_\tau h_\tau(\tau_k)$ is a Euclidean gradient.
Consider a reparametrization $\lambda$ so that $\lambda=\mathbf{U} \tau$, where $\mathbf{U}$ is a constant (square) invertible matrix.
$$
\begin{aligned}
\min_{\lambda \in \mathcal{R}^K } h_\lambda(\lambda):= h_\tau( \mathbf{U}^{-1} \lambda)
\end{aligned}
$$
The Euclidean gradient descent (GD) in parametrization $\lambda$ is
$$
\begin{aligned}
\lambda_{k+1} \leftarrow \lambda_{k} - \alpha {\mathbf{g}}_{\lambda_k}
\end{aligned}\tag{6}\label{6}
$$ where ${\mathbf{g}}_{\lambda_k} := \nabla_\lambda h_\lambda(\lambda_k)$ is a Euclidean gradient.
Note that Euclidean gradients follow the transformation rule as
$$
\begin{aligned}
\mathbf{g}_\tau^T = \mathbf{g}_\lambda^T \mathbf{J}
\end{aligned}
$$ where $J_{ki}:=\frac{\partial \lambda^k(\tau) }{ \partial \tau^i }$
We can verify that $\mathbf{J}=\mathbf{U}$ and $\mathbf{g}_\tau = \mathbf{U}^T \mathbf{g}_\lambda $.
Notice that $\tau_0 = \mathbf{U}^{-1} \lambda_0$ by construction.
The update in $\eqref{5}$ at iteration $k=1$ then can be re-expressed as
$$
\begin{aligned}
\tau_{1} \leftarrow \tau_{0} - \alpha {\mathbf{g}}_{\tau_0} = \mathbf{U}^{-1} \lambda_0 - \alpha \mathbf{U}^{T} {\mathbf{g}}_{\lambda_0} \neq \mathbf{U}^{-1} \lambda_1
\end{aligned}
$$
It is easy to see that
updates in $\eqref{5}$ and $\eqref{6}$ are NOT equivalent.
Therefore, Euclidean gradient descent is not invariant.
Newton’s Method is Linearly Invariant
For simplicity, consider an unconstrained convex optimization problem.
$$
\begin{aligned}
\min_{\tau \in \mathcal{R}^K } h_\tau(\tau)
\end{aligned}
$$ where $h_\tau(\tau)$ is strongly convex and twice continuously differentiable w.r.t. $\tau$.
Newton’s method under parametrization $\tau$ is
$$
\begin{aligned}
\tau_{k+1} \leftarrow \tau_{k} - \alpha \mathbf{H}^{-1}_\tau(\tau_k) {\mathbf{g}}_{\tau_k}
\end{aligned}
$$ where ${\mathbf{g}}_{\tau_k} := \nabla_\tau h_\tau(\tau_k)$ is a Euclidean gradient and $\mathbf{H}_\tau(\tau_k):=\nabla_\tau^2 h_\tau(\tau_k)$ is the Hessian.
Consider a reparametrization $\lambda$ so that $\lambda=\mathbf{U} \tau$, where $\mathbf{U}$ is a constant (square) invertible matrix.
$$
\begin{aligned}
\min_{\lambda \in \mathcal{R}^K } h_\lambda(\lambda):= h_\tau( \mathbf{U}^{-1} \lambda)
\end{aligned}
$$ where $h_\lambda(\lambda)$ is also strongly convex w.r.t. $\lambda$ due to $\eqref{7}$.
Newton’s method under parametrization $\lambda$ is
$$
\begin{aligned}
\lambda_{k+1} \leftarrow \lambda_{k} - \alpha \mathbf{H}^{-1}_\lambda(\lambda_k) {\mathbf{g}}_{\lambda_k}
\end{aligned}
$$ where ${\mathbf{g}}_{\lambda_k} := \nabla_\lambda h_\lambda(\lambda_k)$ is a Euclidean gradient and
$\mathbf{H}_\tau(\lambda_k):=\nabla_\lambda^2 h_\lambda(\lambda_k)$ is the Hessian.
As we discussed in the previous section,
Euclidean gradients follow the
transformation rule as $\mathbf{g}_\tau^T = \mathbf{g}_\lambda^T \mathbf{J}$, where
$\mathbf{J}=\mathbf{U}$.
Surprisingly, for a linear transformation, the Hessian follows the transformation rule like the FIM as
$$
\begin{aligned}
\mathbf{H}_{\tau} (\tau_k) &= \nabla_\tau ( \mathbf{g}_{\tau_k} ) \\
&=\nabla_\tau ( \mathbf{J}^T \mathbf{g}_{\lambda_k} ) \\
&=\mathbf{J}^T\nabla_\tau ( \mathbf{g}_{\lambda_k} ) + \underbrace{[\nabla_\tau \mathbf{J}^T ]}_{=0} \mathbf{g}_{\lambda_k} \,\,\,\,\text{(In linear cases, } \mathbf{J} = \mathbf{U}\text{ is a constant)} \\
&=\mathbf{J}^T [ \nabla_\lambda ( \mathbf{g}_{\lambda_k} ) ] \mathbf{J} \\
&=\mathbf{J}^T \mathbf{H}_{\lambda} (\lambda_k)\mathbf{J}
\end{aligned}\tag{7}\label{7}
$$
Therefore, the direction in Newton’s method denoted by $\tilde{\mathbf{g}}_{\tau_k} := \mathbf{H}^{-1}_\tau(\tau_k) \mathbf{g}_{\tau_k}$ is transformed like natural-gradients in linear cases as
$$
\begin{aligned}
\tilde{\mathbf{g}}_{\tau_k} &:= \mathbf{H}^{-1}_\tau(\tau_k) \mathbf{g}_{\tau_k} \\
&= [ \mathbf{J}^T \mathbf{H}_{\lambda} (\lambda_k)\mathbf{J} ]^{-1} \mathbf{g}_{\tau_k} \\
&= \mathbf{J}^{-1} \mathbf{H}^{-1}_{\lambda} (\lambda_k)\mathbf{J}^{-T} [ \mathbf{J}^{T}\mathbf{g}_{\lambda_k} ] \\
&= \mathbf{J}^{-1} \mathbf{H}^{-1}_{\lambda} (\lambda_k) \mathbf{g}_{\lambda_k} \\
&= \mathbf{J}^{-1} \tilde{\mathbf{g}}_{\lambda_k} \\
&= \mathbf{Q} \tilde{\mathbf{g}}_{\lambda_k} \\
\end{aligned}
$$ where by the definition we have $\mathbf{Q}= \mathbf{J}^{-1}$.
The consequence is that Newton’s method like natural-gradient descent is linearly invariant.
The Hessian is not a valid manifold metric
The Hessian $\mathbf{H}_\tau(\tau_k)=\nabla_\tau^2 h_\tau(\tau_k)$ in general is not a valid manifold metric since it does not follow the transformation
rule of a metric in non-linear cases3.
Contrastingly, the FIM is a valid manifold metric. Recall that the FIM can also be computed
as
$\mathbf{F}_\tau(\tau) = E_{p(w|\tau)}\big[ -\nabla_\tau^2 \log p(w|\tau) \big]$.
Claim:
The FIM follows the transformation rule even in non-linear cases.
Proof of the claim (click to expand)
We will discuss in
Part V, for a special parametrization $\tau$ (known as a natural parametrization) of exponential family, the FIM under this parametrization can be computed as
$\mathbf{F}_\tau(\tau) = \nabla_\tau^2 A_\tau(\tau)$, where $A_\tau(\tau)$ is a strictly convex function.
In the literature, the exponential family with a natural parametrization is known as a Hessian manifold [5], where the FIM under this kind of parametrization is called a Hessian metric. However, a non-linear reparametrization will lead to a non-natural parametrization.
References
[1] S.-I. Amari, "Natural gradient works efficiently in learning," Neural computation 10:251–276 (1998).
[2] C. Atkinson & A. F. S. Mitchell, "Rao’s distance measure," Sankhyā: The Indian Journal of Statistics, Series A 345–365 (1981).
[3] M. E. Khan, R. Babanezhad, W. Lin, M. Schmidt, & M. Sugiyama, "Faster stochastic variational inference using Proximal-Gradient methods with general divergence functions," Proceedings of the Thirty-Second Conference on Uncertainty in Artificial Intelligence (2016), pp. 319–328.
[4] F. Kunstner, P. Hennig, & L. Balles, "Limitations of the empirical Fisher approximation for natural gradient descent," Advances in Neural Information Processing Systems 32:4156–4167 (2019).
[5] H. Shima, The geometry of Hessian structures (World Scientific, 2007).
Footnotes:
-
Informally, we locally identify the parameter space with the tanget vector space. However, not all properties are the same in these two spaces. For example, the weighted inner product induced by the Riemannian metric is only defined in the vector space. We often do not use the same weighted inner product in the parameter space. ↩
-
In Riemannian geometry, a geodesic is induced by the Levi-Civita connection. This connection is known as the metric compatiable parallel transport. Christoffel symbols are used to represent the connection in a coordinate/parametrization system. ↩
-
This is due to the non-zero partial derivatives of the Jacobian matrix (Eq. \eqref{7}) when it comes to non-linear parameter transformations. These partial derivatives are also related to Christoffel symbols or Levi-Civita connection coefficients. ↩